| 横浜サイエンスフロンティア中学校 適性検査Ⅰの問題と解答 |
| 横浜サイエンスフロンティア中学校 適性検査Ⅱの問題と解答 |
| 中山学院 トップページ |
↑ ご質問等は上記までメール・お電話にて、お尋ねください。
| 横浜SFjH 適性検査 Ⅰ・Ⅱ 塾長解説 |
令和7年度
適性検査Ⅰ
問題1 「資料1」~「資料3」は会話文1中の下線部の①に描かれている人物に関連する資料です。各資料が表している 人物の説明として最も適切なものを、次の1~6から一つずつ選び、番号を書きなさい。 1 十代の頃に和歌の塾に通い、その後女性の目から見た社会を小説「たけくらべ」などに書きあらわした。 2 欧米の文化を取り入れつつ、国内の産業の発展に力を尽くし、教育機関の設立にも関わった。 3 当時の日本最年少の留学生として外国に渡り、帰国後は女性の地位向上のために力を尽くした。 4 医学の研究を重ね、衛生学などの発展に貢献するとともに、多くの医学者を育成した。 5 新しい文化や考え方を「学問のすすめ」という書物にまとめたり、大学を創設したりした。 6 黄熱病の研究のため中南米やアフリカの地域に渡り、世界の感染症研究に貢献した。 資料1は、新1万円札の渋沢栄一。 資料2は、新五千円札の津田梅子。資料3は新千円札の北里柴三郎です。 よって、答えは、資料1は2番 資料2は、3番、資料3は4番です。 ※ 1番は、旧五千円札の樋口一葉 5番は、旧一万円札の福沢諭吉 6番は旧千円札の野口英世です。 問題2 「資料4」~「資料6」を見て、「資料4」のXの色として最も適切なものを、次の1~6から一つずつ選び、番号を書きなさい。 資料6の地図から、資料4のピクトグラムは、標高の低い所と高いところの境界に設置されています。よって、これは津波などの災害から高台に非難するように勧告しているものと考えられます。 資料5でそれに該当する意味が記されている色は緑の4番です。  credit 災害新聞 ※ 参考 津波を起こす地震は、海溝型といって震源は海洋プレートと大陸プレートがぶつかり合っている海底です。その境目では、1年に数cmほどの割合で海洋プレートが、大陸プレートを引きずり込みながらその下にもぐりこんでいきます。それにより、数十年から数百年をかけて大陸プレートは引っ張られ、ひずみが徐々にたまっていきます。 そしてある時、限界を超えると海底にある大陸プレートは耐えきれなくなり、跳ね上がります。それによって、大量の海水が上昇し、海面が持ち上げられ津波が発生します。2011年の東日本大震災はこの海溝型地震でした。 静岡駿河湾沖から九州南部にかけて、今後発生が予想されている南海トラフ地震も海溝型です。ハザードマップなどをよく見て、普段から津波対策について考えておく必要があります。 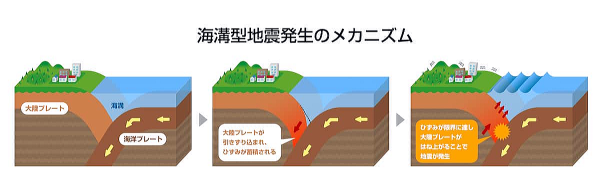 credit 災害新聞 問題3 「資料6」のAからBまでの実際の直線距離として最も適切なものを、次の1~4から一つずつ選び、番号を書きなさい。 1 約100m 2 約500m 3 約1000m 4 約1500m 「資料6」の地図500mが5cmに表されています。地図上でAからBまでは、約10cmなので、答えは3番です。 問題4 「会話文3」中の下線部②について、この浮世絵「資料7」が描かれた時期の説明として最も適切なものを、次の1~4から一つずつ選び、番号を書きなさい。 1 京都に幕府が置かれた時期で、雪舟によって水墨画が描かれた。 2 都の貴族が力をもった時期で、かな文字を使って文学作品がつくられた。 3 聖武天皇が国を治めた時期で、正倉院に外国から伝わった品物を保存した。 4 大都市で町人の文化が栄えた時期で、杉田玄白らがオランダの医学書を翻訳した。 資料7の浮世絵は、葛飾北斎が描いた「富嶽三十六景神奈川沖浪裏」です。これは江戸時代後半の化政文化の時の作品です。よって、同時代に活躍したのは、杉田玄白なので、答えは4番です。 富嶽三十六景神奈川沖浪裏  credit 国立文化財機構 ※ 1は、室町文化 2は、国風文化(平安時代) 3は、天平文化(奈良時代)です。 問題5 「会話文4」を読み、( あ )にあてはまる文として最も適切なものを、次の1~4から一つずつ選び、番号を書きなさい。 1 その国では実在していなかったもの 2 その国に住む人々が生活している様子 3 その国ではまだ知られていないもの 4 その国の文化や歴史など、国を象徴するもの 「資料8」から、南アフリカ・エジプト・ネパールの紙幣にはそれぞれ、動物・スフィンクス・エベレストが描かれています。よって、答えは4番です。 問題6 ポールさんの国と面している「資料9」のZの海洋名称を漢字3字で書きなさい。 「資料9」からポールさんの国は、フランスとわかります。その西に広がる海洋は、大西洋です。 問題7 「会話文4」を読み、( い )にあてはまる文として適切ではないものを、次の1~4から一つ選び、番号を書きなさい 1 地球環境への配慮 2 国と国との交流 3 国同士の対等な関係 4平和な未来 「会話文4」の中で、みなみさんのセリフ「よく見ると、すべてのお札に橋が描かれていますね。」 「お札にも様々な思いが込められているのですね。」とあります。 ユーロが、ヨーロッパの国々の共通通貨として使われているのと同様に、「橋」は国同士が現在から将来に渡り、自由に行き来できる相互関係の象徴として描かれています。よって、ふさわしくないのは1番になります。
問題1 「資料2」の「ひっきりなしに次々と本を読み、後から考えずにいると、せっかく読んだものもしっかり根を下ろさず、ほとんどが失われてしまう」とはどういうことですか。最も適切なものを、次の1~4から一つ選び、番号を書きなさい。 1 栄養をまったくとらないでいると、胃が悪くなり身体全体がだめになってしまうということ。 2 本を買うという行いだけで、その内容も一緒に理解した気持ちになってしまうということ。 3 他人の考えを絶えず押しつけられると自分で考えることをだんだんしなくなるということ。 4 紙に書きあらわされ思想は、実際に自分の目で確かめてみないと分からないということ。 8行目から10行目かけて、「おそろしくたくさん本を読んでいると、何も考えずに暇つぶしができて、骨休みにはなるが、自分の頭で考える能力がしだいに失われていく」とあります。 よって、答えは3番です。 問題2 筆者である茂木健一郎さんとショーペンハウアーさんは、どのように本を読めばよいと考えていますか。「資料1」、「資料2」から、次の条件、書き方の注意にしたがってそれぞれ書きなさい。 条件 1 それぞれ170字以上200字以内で書くこと。 2 どのように読めばよいかを先に書き、後にその理由を書くこと。 書き方の注意 1 題名、名前は書かないこと。 2 段落は作らず、1マス目から書くこと。 資料1の解答例 さまざまな視点で描かれた小説や物語などのフィクション作品を登場人物の視点や感情に焦点をあてて読む。現代社会では価値観が多様化し、他者と協調していくことが求められている。そのために必要とされるのが、想像力と共感力である。小説や物語は背景・情景・行間のニュアンスを読み取るために想像力が養われ、共感力が鍛えられる。それは思考力の強化につながり、自分の言動や態度などを選択できる能力を備えることができる。 199字 資料2の解答例 絶えず読むのではなく、読んだことを必ず後で自分で考えてみる読み方をする。読書は他人にものを考えてもらうことであり、紙に書かれた思想は砂に残った歩行者の足跡以上のものではない。だが、歩行者が何を見たかを知るには自分の目を用いなければならない。自分の頭で熟慮を重ねることによってのみ、読まれたものは真に読者のものとなる。読み続けるだけでは考える時間が失われ、心の中には何も残らないからである。 196字 |
適性検査 Ⅱ
問題1 「資料1」の中の( あ )にあてはまる最も適切な言葉を「資料1」から抜き出して書きなさい。 1号転てつ機を動かすためには、転てつカンが動くようにします。それには信号カンの切り欠きが、転てつカンの 場所へくる必要があるので、「停止」の方向へ動かします。 よって、( あ )にあてはまる言葉は、停止です。 問題2 FSが利用されている場面は次の1~5のうちどれですか。あてはまるものをすべて選び、番号を書きなさい。 1 エレベーターで一定速度以上の落下時に、非常止め装置が作動する。 2 電子レンジで温度センサーが故障して特定の温度を超えてしまったとき自動的に電源が切れる。 3 踏切遮断機は故障しても自動的に遮断かんが降りる。 4 石油ストーブをつけているとき、ストーブが転倒すると自動的に消える。 5 自動車でブレーキを踏んだ状態のときにだけエンジンを始動することができる。 「資料2」の中に、FSの例は、「装置故障時、異常発生時に・・・」とあります。 5以外はすべてそれにあてはまります。よって答えは、1・2・3・4になります。 問題3 「図7」のようにスイッチボタンを押してからランプが点灯するまでの間のリレー内での作動順序Aと、「図8」の ようにスイッチボタンをはなしてからランプが消灯するまでの間のリレー内での作動順序Bに、あとの1~9から あてはまるものをすべて選び、それらについて番号を順序通りに書きなさい。 Aは、図7を見て答えます。コイルに電流が流れると4の鉄芯が磁石になります。すると上の鉄片が引きつけら れます。それによって、可動接点が動いて固定接点に接触してONの状態になり、電流が流れます。 よって、答えは 4→3→7 です。 Bは、図8を見ます。コイルの電流がなくなると、鉄片を引きつけることができなくなりバネの力で鉄片が鉄芯 からはなれます。すると可動接点が固定接点からはなれ、OFFの状態になります。 よって、答えは 5→6 です。 問題4 電圧が足りないと可動接点が動かない理由を、次の文の( い )( う )( え )に最もよくはてはまる言葉 を入れて答えなさい。 ( い )の( う )が( え )から 「資料4」のコイルの電源を調整していく実験で、「ある程度電圧を下げると可動接点がOFFになって、ランプが 消灯することがわかりました。」とあります。 答えは、( い )がコイル ( う )が鉄片を引きつける力 ( え )が小さい です。 問題5 次の文の( お )( か )( き )に最もよくはてはまる数を入れて答えなさい。 この実験から可動接点をONにしてランプを確実に点灯させるためには、少なくとも( お )V以上の電圧が 必要となることがわかりました。 また、ONの状態を維持するためには、少なくとも( か )V以上の電圧が必要となることがわかりました。 リレーを正しく作動させるためには、「資料4」で用いた乾電池(1.5V)を少なくとも( き )本を使用し、 直列につなぐ必要があります。 確実に点灯させるためには、表1の10回目の実験の数値の、7.55V以上が必要です。 ONの状態を維持するためには、表2の実験で可動接点がOFFになる最高値が5回目と6回目の3.40が 最高なので、少なくとも3.41V以上の電圧が必要です。 また、乾電池1本は1.5Vなので、7.55以上の電圧を得るためには、1.5×6=9で 6本を直列に つなぐ必要があります。 よって、答えは ( お )が 7.55、 ( か )が 3.41、 ( き )が 6 です。 問題6 「図9」のように導線をつないだ回路をつくりました。スイッチボタンを一度押し、はなしました。さらに、もう一度 スイッチボタンを一度押し、はなしました。この後1分間、ランプはどのような状態になるか5~15字以内で 書きなさい。 図9の回路では、スイッチボタンを一度押して、はなすと可動接点がONになり、すべての回路がつながった 状態が続きます。よってそれ以降ボタンを押したり、はなしたりしてもランプはついたままになります。 答えは、点灯したままの状態になる です。
たろうさんとはなこさんは、立体の中にできる立体について考えています。 次の会話文を読み、あとの問題に答えなさい。ただし、図は正確とは限りません。 問題1 「図1」でできたピラミッドのような「立体A」一つ分の体積を求めなさい。 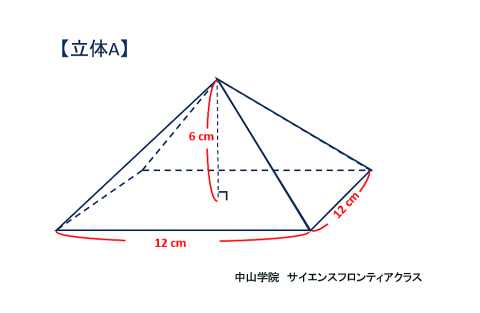 立体Aは四角錐で、底面が1辺12cmの正方形 高さが6cmです。 角錐の体積の求め方は、底面積×高さ×1/3(÷3)なので、12×12×6×1/3=288 答え 288cm3です。 問題2 「図3」で立方体の中にできた「立体B」の体積を求めなさい。 立体Bの解き方を説明します。 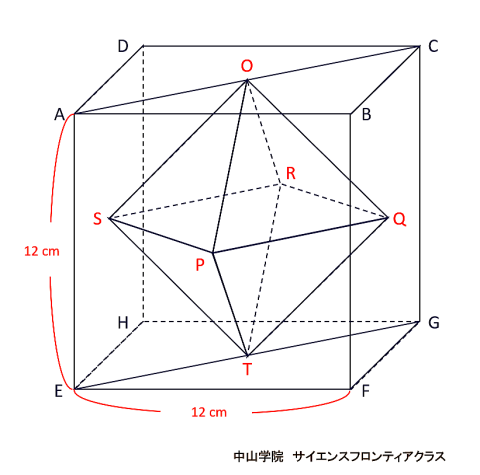 立方体の中にある正八面体を、OーPQRSーTとします。正八面体の中央にある正方形PQRSの対角線PRと 対角線QSは、それぞれ12cmです。正方形の面積はひし形の面積の公式で求めることができるので、 12×12÷2=72cm2です。上下の四角錐を合わせた高さは12cmなので、72×12×1/3=288 答え 288cm3になります。 簡単な公式で求めることもできます。 それは、立方体の体積×1/6 (÷6) です。 12×12×12×1/6=288 で求められます。 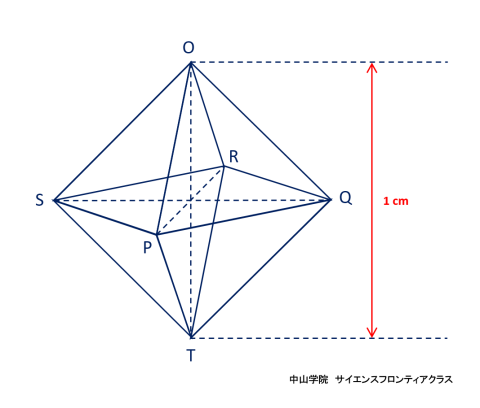 正八面体の高さOTを1cmとします。 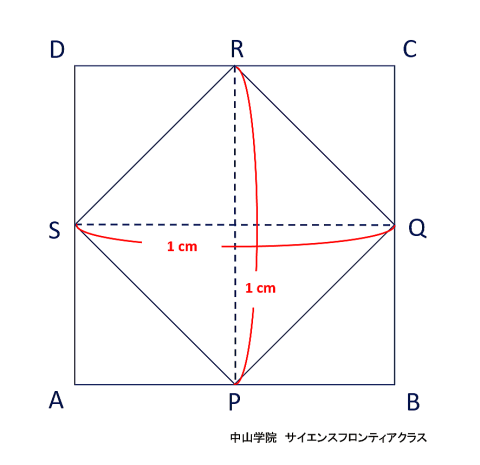 中央の正方形の対角線PR・SQも1cmになります。 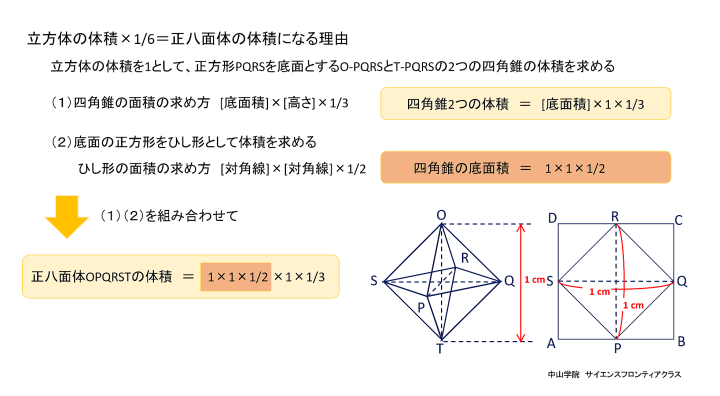 立方体の体積を1cm3とすると、立方体の中にできる正八面体の体積は、1/6cm3になります。 問題3 「会話文の続き」 はなこさん: 学校の授業では、粘土で立方体をつくり、その立方体を切って観察しましたね。同じように、この「図3」の立体 をななめに切ると、その切った面はどうなるでしょうか。 たろうさん: ななめに切るとはどういうことですか。 はなこさん: 「図4」のように、立方体の面ABCDの対角線ACと面EFGHの対角線EGを通る平面で切ることです。 問題 「図4」のように切ったときの面AEGCのようすとして最も適切なものを、次の1~5から一つ選び、番号を書き なさい。ただし、1~5の内側の図形は、1は長方形、2は正方形、3と4はひし形、5は六角形とします。 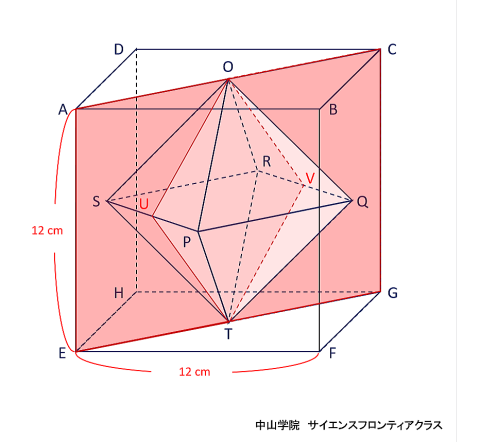 対角線ACと対角線EGを通る平面で切ると長方形になります。(ピンクの部分) 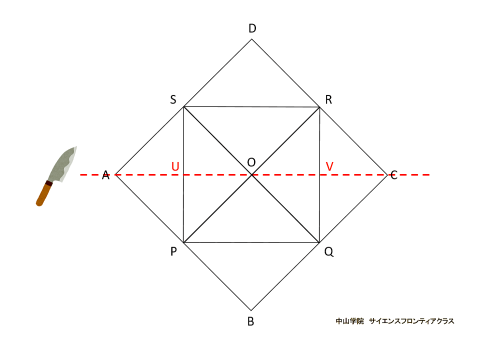 SPとQRの中点を、それぞれUとVとします。 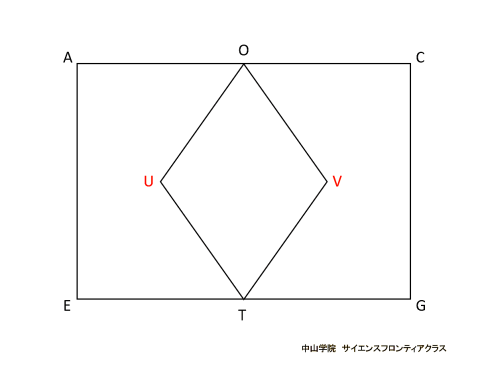 すると、四角形OUTVはひし形となり、UVはOTよりも短くなります。 よって、答えは4番です。 問題4 「会話文の続き」 たろうさん: 立体の中にできる立体を考えるといろいろな発見がありますね。 はなこさん: そうですね。もっと調べていきましょう。「図3」で中にできた8つの面で囲まれた立体で、となりあう面の真ん中 同士をさらに直線でむすんだところを想像してみましょう。 たろうさん: あれ、また立方体ができました。 はなこさん: 興味深いですね。この状態で真上から見るとどのように見えるか図にかいてみましょう。 問題 次の「図5」は、上の会話文の「どのように見えるか図にかいてみましょう。」のあとにかいた図です。 ただし、途中までしかかかれていません。真上から見たときに見える辺をすべてかき加えて解答らんの図を 完成させなさい。 図4に、問題4の会話文に沿ってその内容を書き加えた立体図です。 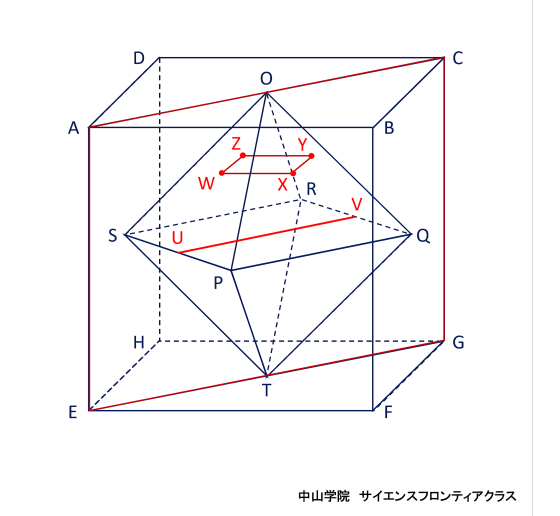 図4の立方体の面ABCDを真上から見ると、OとTが重なります。また、辺ABの中点がP,辺BCの中点がQ、 辺CDの中点がR、辺DAの中点がSとなります。するとPとR、QとSをむすんだ線をかくことができます。 また、辺AB・辺BC・辺CD・辺DAに平行に、短い辺 WX・XY・YZ・ZWで構成される正方形ができます。 正八面体の下半分の四角錐にも同様の正方形(省略)ができますが、真上から見ると重なって見えます。 図5の解答です 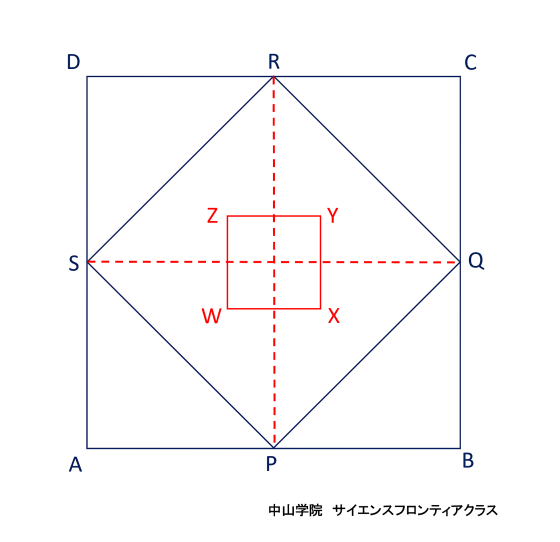 図5にかいていきましょう。最初にかき加えるのは、PとR、QとSをむすんだ線です。(実際は実線でかきます) 会話文の中に、「8つの面で囲まれた立体で、となりあう面の真ん中同士をさらに直線でむすぶと立方体が できた。」とあります。 それを真上から見ると、上図のように小さな正方形WXYZが中央に位置するので、その正方形をかき加えて、 完成です。 問題5 「会話文」の続き たろうさん: 6つの面で囲まれた立方体から8つの面で囲まれた立体ができて、またその中に立体ができます。これをくり 返していくと面白そうですね。 はなこさん: そうですね。他の立体でも同じことをやってみませんか。 たろうさん: では、この「図6」の立体はどうでしょうか。 はなこさん: この立体はすべての面が正五角形です。 たろうさん: この立体で、となりあう面の真ん中同士を直線でむすんだところを想像するとどんな立体ができる でしょうか。見取り図をかいてみましょう。 はなこさん: また、興味深い立体の見取図がかけました。 問題 「図6」の立体で、となりあう面の真ん中同士を直線でむすんだときにできる立体の①面の数、②頂点の数 をそれぞれ答えなさい。 問題5の内容に沿ってかいた、となりあう面の真ん中同士を直線でむすんだときにできる図6の立体です。 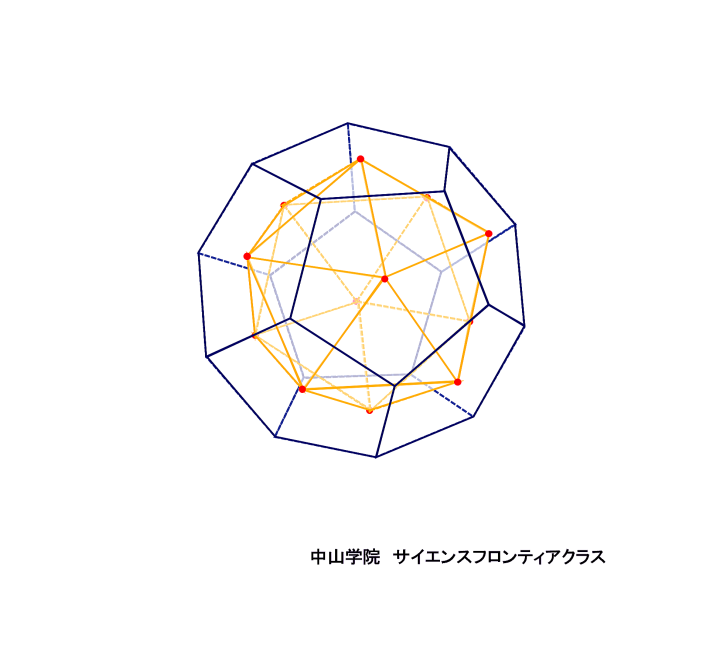 一つの面が正五角形の正十二面体の中に、一つの面が正三角形の正二十面体ができます。 答え ①の面の数は、20 ②の頂点の数は、12です。 問題文で「となりあう面の真ん中同士を直線でむすんだとき」とありますので、上の図から頂点の数は図6の 面の数(真ん中同士をむすぶ前)と等しくなることがわかります。それに気がつくと簡単に答えがでます。 図6で真ん中同士を直線でむすぶ前の立体は、すべての面が正五角形の正十二面体です。(数えても12個 あります) よって②の頂点の数は面の数と等しいので、②の答えは12です。(※参照) ※ 正十二面体のとなりあう面の真ん中同士を直線でむすんで出来た正二十面体の一つ一つの面の形は 正三角形です。一つの三角形の頂点の数は3個で、それが20面あるので、バラバラにすると合計60個です。 しかし、正二十面体の一つの頂点には正三角形の5面の頂点が集まっています。三角形の5つの頂点が接 して多面体の一つの頂点になっています。よって、60÷5=12で、正二十面体の頂点の数は12個です。 さて、「図6」の立体で、となりあう面の真ん中同士を直線でむすんだときにできる立体は何かというと、頂点が 12個で、20個の正三角形で囲まれた正二十面体です。 会話文の中に、「興味深い立体の見取図がかけました。」とありますが、かくのはちょっと大変でした。 答え ①の面の数は20です。 ※ 参考 正多面体のまとめ
【 辺・頂点の数・頂点に集まる面の数を公式で求める方法 】 ( 1 ) 辺の数 = 1つの面の辺の数×面の数÷2 ( 2 ) 頂点の数 = 辺の数-面の数+2 ( 3 ) 1つの頂点に集まる面の数=辺の数×2÷頂点の数 例 正二十面体の場合 (1) 辺の数=3×20÷2=30 (2) 頂点の数=30-20+2=12 (3) 1つの頂点に集まる面の数=30×2÷12=5 問題6 厚紙でつくられた「図6」の立体を、「図9」と同じように、となりあう2つの頂点が重なって見えるように見た ときの、見える面の数を答えなさい。 下の図6の立体を頂点Aと頂点Bが重なって1つの点に見えるように見たとします。 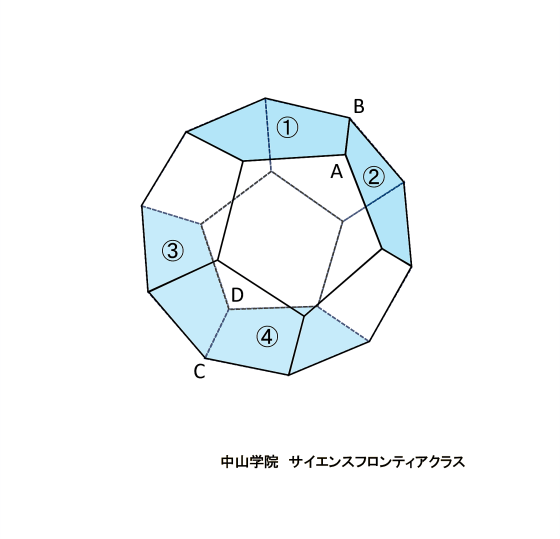 図6の正十二面体に頂点Aと頂点Bをとり、正面から見て頂点Aと頂点Bが重なって見えるように置きます。 その際に、頂点Aが手前にくるようにします。 すると、辺ABを一辺とする正五角形①・②は見えません。また辺ABに平行な辺を辺CDとすると、同様に CDを一辺とする正五角形③・④も見えません。 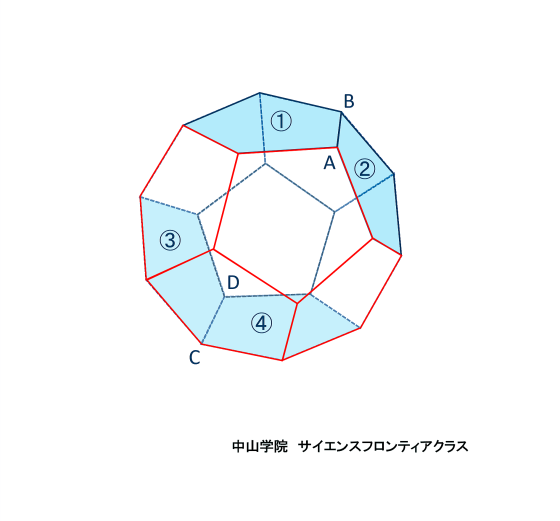 よって、面①②③④より手前にある面(図の赤線で囲まれた部分4面)は見えますので、答えは4です。 立体工作授業  実際に正十二面体を作って確かめてみました。 完 |
| 適性検査 ⅠⅡ 塾長解説 |
令和6年度
| 適性検査 Ⅰ ※ 今年の検査Ⅰは、例年と比較すると難易度がやや下がりました。
問題1 「会話1」中の①「太陽の出ない季節」という言葉が使われている地域として最も適切な地域を次の「地図中の1~4から一つ選び、番号を書きなさい。 答えは、1です。 資料2の図から、地球が自転しても北極周辺は1日中、太陽の光が当たらないことがわかります。このよ うなことが起こるのは、地軸が地球の公転面の垂線に対して約23.4度傾いているからなのです。 1日中、太陽が出てこない現象を極夜(きょくや)といいます。反対に1日中、太陽が出ている現象もあります。白夜(びゃくや)と言います。皆さんもどこかで耳にしたことがあると思います。 極夜・白夜が起こるのは、緯度(赤道が0度、北極・南極が90度)が66.6度(90度-23.4度)以上の地域に限られます。北緯66.6度以上を北極圏、南緯66.6以上を南極圏といいます。 よって、地図でスカンジナビア半島の上部は、北極圏の地域に当てはまりますので、答えは1になります。 「極夜・白夜は、スウェーデンやフィンランドの北部地域で起きる現象である」ということを知っていた生徒さんは、すぐに答えを書けたのではないでしょうか ※南極圏の地域は選択肢にありません。 問題2 「会話2」中の②にあてはまる気温と降水量のグラフを次のAとBから選び、「会話2」中の③にあてはまる作物との組み合わせとして適切なものを、「資料5」~「資料7」を参考にしてあとの1~6から一つ選び、番号を書きなさい。 答えは、1です。 「マレーシアやシンガポールと同じ気候の地域」とありますので、気候のグラフは、Aの1年中高温・多雨の熱帯雨林とわかります。また、小麦・オリーブ・コーヒーのうち、熱帯で栽培されている作物はコーヒーです。よって答えは、1の「Aとコーヒー」になります。 問題3 「資料8」を参考にして、672年と1868年に起こったできごとを次の1~6から,それぞれ一つずつ選び、番号を書きなさい。 答えは、672年は、5の「壬申の乱」、1868年は、4の「戊辰戦争」です。 この問題は、「資料8」を参考にしなくても、今回受験された皆さんなら即、わかったと思います。答えの時間を節約できましたね。受験生にとって年号は必修事項で壬申(じんしん)の乱、戊辰(ぼしん)戦争は、小学校で学ぶ歴史の中でも最も重要な出来事の一つです。これから受験する生徒の皆さんは、主な年号は全て、覚えておく必要があります。 ※ ちなみに「資料8」を利用した解き方を説明しておきます。 672÷10=67・・・2 十干で、余り2は、「壬」です。 672÷12=56・・・0 十二支で余り0は、「申」です。 よって、答えは「壬申」です。 1868÷10=186・・・8 十干で、余り8は、「戊」です。 1868÷12=155・・・8 十二支で余り8は、「辰」です。 よって、答えは「戊辰」になります。 問題4 答えは、4です。 「資料9」中の④下関条約が結ばれたところがある県と⑤門司港がある県の2つの県以外で起こったことを次の1~4から一つ選び、番号を書きなさい。 ④の下関条約が結ばれたところは、山口県です。また、⑤の門司港がある県は福岡県です。 選択肢1 中国(漢)の皇帝から与えられた金印が発見された。 ⇒ 福岡県 選択肢2 源氏が壇ノ浦の戦いで平氏をほろぼした。 ⇒ 山口県 選択肢3 元との戦いに備えて防塁がつくられた。 ⇒ 福岡県 選択肢4 ポルトガル人が漂着し、鉄砲が伝わった。⇒ 鹿児島県(種子島) 歴史の知識が問われる問題でした。 よって答えは4です。 問題5 「会話4」中の⑥にあてはまる言葉として最も適切なものを次の1~4から一つ選び、番号を書きなさい。 答えは、2です。 「会話4」の中のみなみさんの言葉がヒントになります。「今では当たり前のように思えることも、昔はちがったのですね。」という部分です。 今では、義務教育により、ほぼ100%の子どもが小学校に通っています。このことが「今では当たり前」の箇所に照応しています。 よって、答えは、2の「学制にもとづいて小学校に通った子どもの割合の変化」になります。 参考資料: 明治政府が、1872年(明治5年)に学制を発布して、6歳以上の子どもに教育を受けさせることを国民の義務とし、全国各地に小学校を造りました。しかし、初めのうちは授業料を負担できず、学校に行けない子どもが大勢いました。 就学率は30%程度で、それもほとんどが男子でした。特に女子は「家事の担い手として必要である。」という考えもあり、就学率はなかなか上がりませんでした。 それでも、1875年には女子が20%近くまでになり、男子は50%を超えました。1890年になると、女子は、30%、男子は70%になり平均すると50%で、問題の「資料10」に合致します。 その後は女子の就学率が急激に上昇し、1910年には男女とも100%近くになり、ほぼ全ての子どもが小学校に通うようになりました。 すぐに答えが思い浮かばなかった時は、消去法で消していきます。1は、徴兵制で100%が間違っています。1890年頃でも、3~4%程度です。2は、殖産興業で働いていたのは主に女性なので、数字と合いません。 4は、四民平等によって平民とされた人の割合とありますが、当初から平民は90%近くを占めていたので、これもグラフとは一致しません。 問題6 りかさんは日本や外国の言葉に興味をもち、さらにくわしく調べることにしました。その際に大切だと考えられることはどのようなことですか。次の条件にしたがって書きなさい。 「会話」の中で、解答につながる文章がいくつかあります。それを参考にしてまとめます。 「会話1」 スペインには「SIESTA(シエスタ・昼の休憩)」という文化があるのですね。 「SOBREMESA(ソブレメサ)」というスペイン語は、「食後に食卓を囲んで、くつろいでおしゃべりをする」という習慣を指す言葉です。 その国の言葉にはその国の文化が反映されているのですね。 「PISAN ZAPRA(ピサンザプラ・バナナを食べるときの所要時間)」はマレーシアやシンガポールなどで話されているマレー語の言葉です。同じ気候の地域で「資料5」の③が育てられていますね。 上の文でのキーワードは、「文化」「習慣」「気候」の3つです。この3つの言葉を使ってまとめると、 答えは、「その国の文化、習慣、気候等を学ぶこと」になります。 「学ぶこと」は「知ること」でもいいですね。
問題1 「科学の研究員が」ー線「筋肉の名前は、とりあえずそんなに気にしなくてもいいんじゃない?」と言ったことをきっかけに、筆者が気づいたこととして最も適切なものを、次の1~4から一つ選び、番号を書きなさい。 答えは3です。 次の箇所がヒントになります。 「筋肉や神経の名前を忘れ、目の前にあるものを純粋な気持ちで観察しなさい」、「解剖の目的は、名前を特定することではない。まずは、純粋な目で観察することこそが、体の構造を理解する上で何より大事なことである。」 「当時の私はこのことに気がついてはおらず」とあり、その後、言われたことをきっかけに、このことに気がついたのです。 よって、答えは3の「生き物の体の構造を理解するには、目の前にあるものをありのままに観察することが重要であること。」が答えになります。 問題2 「資料1」「資料2」に共通する考えを、次の「条件」「書き方の注意」にしたがって説明しなさい。 1 三つの段落で構成し、三百四十字以上四百字以内で書くこと。 2 三つの段落それぞれの内容は次のようにすること。 第一段落 「資料1」「資料2」に共通する考え 第二段落 共通する考えが「資料1」では具体的にどのように述べられているか 第三段落 共通する考えが「資料2」では具体的にどのように述べられているか
ものごとを観察・観賞する際には、知識や情報を優先せず、まず直接自分の目で見ること、そして頭で考えることが大切である。これが共通の考えである。 資料1では、「キリンの体を解剖する時に、以前は教科書に描かれた構造をキリンの中に探し求めるだけだったが、筋肉の名前の特定にこだわることをやめ、遺体に向き合い、筋肉の名前はわからなくてもその筋肉の付着する場所、走行、大きさ、長さを丁寧に観察し、記録していった。頭を使って解剖することができたと実感した。」と述べられている。 資料2では、「ムンクの叫びという画像を東京で見せて感想を聞いたところ、作者の名前や、作品名を答えるなど自分の知っていることを言うだけの人がほとんどだった。一方、オスロでインタビューした時は、自分の感想をいう人が多かった。ただ作品の情報を話すよりも、作品に対してどれくらい自分の言葉で語れるかが豊かな鑑賞につながる。」と述べられている。 |
| 適性検査 Ⅱ ※ 今年は大問が、1・2の2題になりました。2の方は、折り紙を数回折り、重なった状態で一部を切りとり、それを広げた時の図について問う出題でした。私立中学校入試でもよく出されますが、平面空間図形の分析・処理能力が要求される応用問題です。 平成31年度の適性検査Ⅱでは正八面体の問題が出題されましたが、過去の東京大学の入試問題に出されたものと酷似していました。「論理的思考力」+「空間イメージ創造力」+「ひらめき」も必要とされるような問題でした。 右脳を鍛えておくといいかもしれませんね・・
たろうさんは、深海が地球最後のフロンティアと言われていることに興味をもち、調べ学習を進めていました。そこで科学者たちが深海調査をどのように進めてきたのかについてまとめました。次の「資料1」から「資料7」をみて、あとの問題に答えなさい。 問題1 6000m以上の深さの海の面積は何km2か答えなさい。 答えは、4716686km2です。 「資料1」より、海洋の面積は、362822000km2です。そして、深さ6000m以上の海洋の面積の割合は、1.2+0.1=1.3%です。 よって、362822000×0.013=362822×13=4716686km2 になります。 問題2 実験データを適切に扱い、海水1mlが1.03gとするとき、サラダ油1mlは何gか答えなさい。答えがわりきれないときは、小数第3位を四捨五入して、小数第二位まで答えなさい。ただし、おもりの体積については考えないこととします。 答えは、0.92gです。 資料2の5の実験結果は下記の通りです。
上記の表の1回~10回の重さの合計は329gとなり、平均すると329÷10=32.9gとなります。 実験3以降で追加したサラダ油とおもりの重さ(平均)の和と、それと同じ体積の海水の重さは等しいので、サラダ油1mlの重さを□とおくと、□×300+32.9(サラダ油+おもり)=1.03×300(海水)となります。 還元算で求めます。□×300=309(1.03×300)-32.9 で □×300=276.1 になります。よって、□= 276.1÷300=0.920・・・ です。 小数第3位を四捨五入すると、答えは、0.92gとなります。 問題3 トリエスタ号が、タンクに入れたガソリンの体積は133m3でした。この探査艇が海面にあるとき、ガソリンの浮き上がろうとする力で支えられる重さは何kgか答えなさい。ただし、海水1mlは1.03g、ガソリン1mlは0.75gであるとして計算しなさい。答えがわりきれないときは、小数第1位を四捨五入して、整数で答えなさい。 答えは、37240kgです。 1g=0.001kg なので、1.03g=0.00103kg 0.75g=0.00075kg です。よって、ガソリン1mlで、0.00103-0.00075=0.00028kg の重さを支えられます。 1m3=1000000mlなので、 133m3=133000000mlになります。この二つの数字の積が答えになります。 0.00028×133000000=28×1330=37240 です。 問題4
にあてはまる数やことばを答えなさい。 答えは、「あ」は、’1030’ 「い」は、’つぶれて’ です。 資料4 1cm2の板を板の上面から1cmの深さに沈めるとその上に水が1cm3乗っていることになります。1cm3の海水は1.03gであるとして、10000mの深さに1cm2の板を沈めたと考えると 「あ」 kgの水が乗っていることになります。 例えば、発砲ポリスチレン製のカップ麺の容器に6500mの深海と同じ水の重さが加わると容器はすっかり小さくなってしまいます。そのため深海では図7の発砲ポリスチレンの一つひとつの小さな空間が 「い」 しまい、元に戻らなくなります。 10000mは、1cm×1000000なので、1.03g×1000000=1030000g になります。1000g=1kg なので、「あ」=1030kgです。 容器が小さくなると、発砲ポリスチレンはぎゅーと縮まり、その空間はつぶれてしまいます。発砲ポリスチレンには弾性がないので、元に戻らなくなります。よって、こたえは、「つぶれて」 になります。 問題5 9時00分に潜水を開始して、毎分45mで潜航、浮上するとき、水深6480mで行う調査時間は最大で何時間何分か答えなさい。 答えは、3時間12分です。 資料5
「毎分45mで潜航、浮上する」とありますので、往復では、6480÷45×2=288分かかります。288分=4時間48分です。9時00分に潜水を開始するとありますので、17時00分の揚収作業までの時間は8時間になります。よって、調査時間は最大で、8時間-4時間48分=3時間12分となります。 問題6 「図10」~「図12」から読み取れることとして、次の1~9からあてはまるものをすべて選び、番号を書きなさい。 答えは、3・6・8 です。 選択肢1~3は、図10について、4~6は、図11について、7~9は、図12について記しています。 1.水深と海水温は比例の関係になっている。× 3000m以上は変化がありません。 2.水深1000mでの海水温が最も高い。× 水面が最も高くなっています。 3.水深1000mから水面までが最も海水温の変動が大きい。○ 5℃と18℃で差が最大です。 4.水深1000m付近の塩分濃度が最も高い。× 水面が最も高くなっています。 5.水深が深くなればなるほど塩分濃度が上がっていく。× 水深500mまでは減少しています。 6.水深が0mに近いときの塩分濃度が最も高い。○ 0mでは、34.8psuで、最高です。 7.水深が浅いほど音の伝わる速さは遅い。 × 水深1000mが最も遅くなっています。 8.水深1000m付近の音の伝わる速さが最も遅い。○1000mでは1480m/秒で最も遅いです。 9.水深と音の速さは、比例の関係になっている。×初めは減り、その後増えて、比例していません。 よって、正しく述べているのは、3・6・8になります。 問題7 「資料7」の ( う ) ( え ) にあてはまる数を答えなさい。 新型機(2018年)では、初号機と比べて同じ距離でも通信速度が ( う )倍になったので、画像を ( え )秒に1枚送ることができるようになるまで改良され・・・ 答えは、 ( う )は、5 ( え )は2 です。 図13 音響画像伝送装置の性能比較
(う)は図13より、80÷16=5倍です。 (え)は、資料7の文章中に、「初号機は画像を10秒に1枚しか送ることができなかったり・・」とあります。 通信速度が5倍になったので、転送時間は5分の1になります。10÷5=2秒です。
たろうさんとはなこさんは、「図1」について考えています。次の会話文を読み、あとの問題に答えなさい。ただし、図は正確とは限りません。 問題1 「図3」の⑥のように折られた折り紙EFCを、ハサミで切って、折り紙を①の状態まで開くと「図4」のようになりました。どのように切ったか、最も適切なものを、次の1~8から一つ選び、番号を書きなさい。 答えは、5です。 図3の②で、BとDが重なります。 ③・④でAとCが重なります。 ⑤でBとCが重なります。よって、A・B・C・Dが全て1点に重なります。⑤・⑥で、点Fは、AB・BC・CD・DA上の点だとわかります。図4では、その点Fが、消えているので、底辺をECとする直角三角形FECで、辺FC、辺FE上に、頂点Fから等距離になるような点を二つとり、それらを結んだ線分で切れば、図4のようになります。 よって、選択肢5が答えになります。 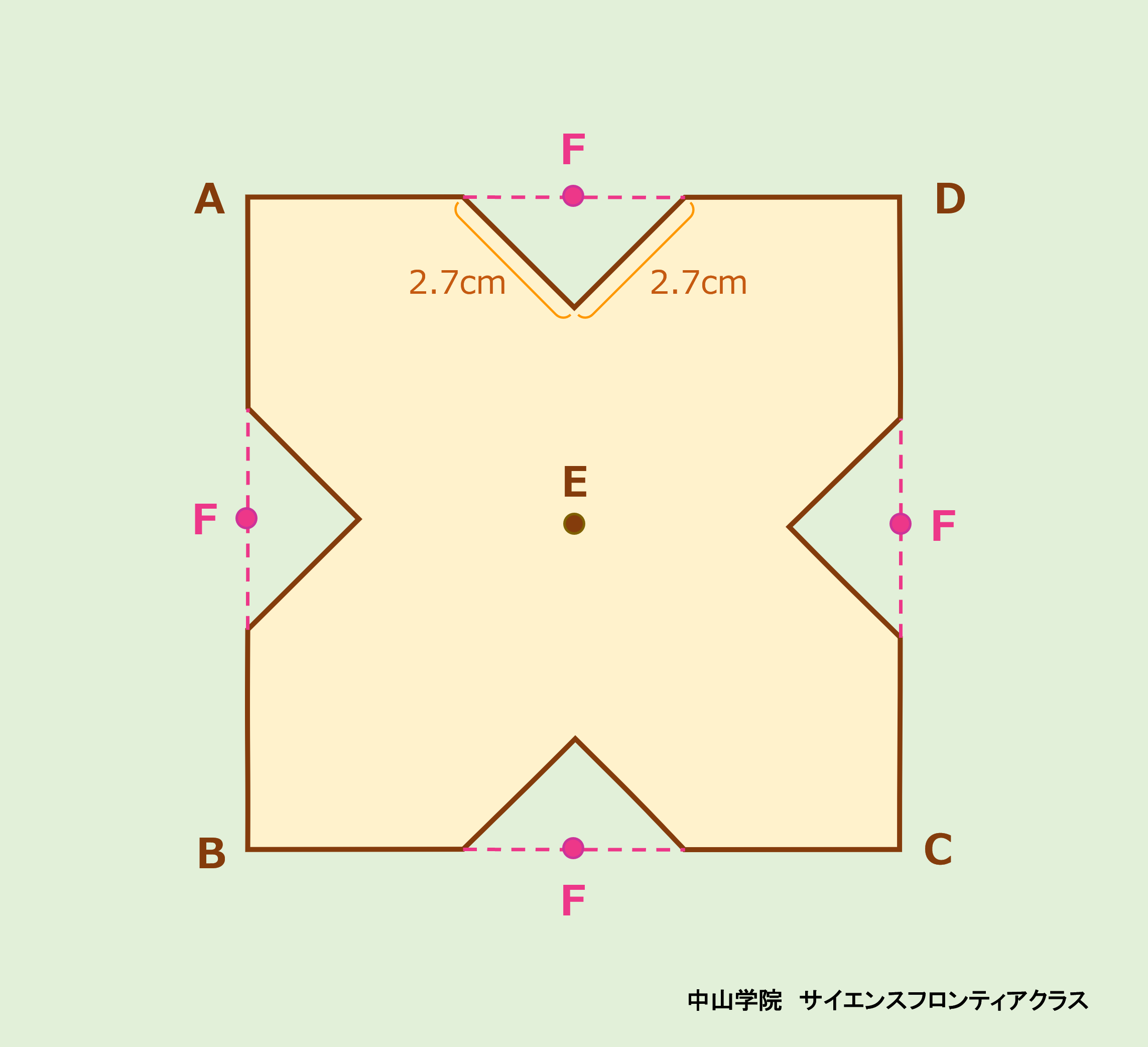 問題2 「図3」の⑥のように折られた折り紙EFCから切り取られた4つの三角形を開いたところ、すべて合同な直角三角形でした。このとき、「図4」の面積は何cm2になるか答えなさい。 答えは、210.42cm2です。 正方形の折り紙から、直角をはさむ2辺が2.7cmの直角二等辺三角形4つを引けば求められます。 正方形は、15×15=225cm2 直角二等辺三角形4つは、2.7×2.7÷2×4=14.58cm2 よって、225-14.58=210.42cm2が答えになります。 問題3 はなこさんは「図3」の⑥のように折られた折り紙EFCを、たろうさんとは別の折り方で、あと1回だけ折ってから、一刀切りをし、折り紙を「図3」の①の状態まで開くと「図6」のようになりました。折り目となる直線を解答用紙の図にかき入れなさい。ただし、解答用紙の図にある点C、E、G、H、I、J、K、L、M、N、Oから、最も適切な2点を選び、まっすぐにつなぐこと。また、G、I、Lはそれぞれ辺EC、EF、FCの真ん中の点とする。 答えは、点Jと点Gをつなぐ 線分JG です。 「図6」で折る前の折り紙ABCDでは、中央の点がE、そこから下へ垂線を引いてBCと交わる点(BCの中点)がFになります。 また、中央の切り取られた小さな正方形では、中心は開いた折り紙と同じ点E、Eから下に引いた垂線が、⑥の図のHになります。そしてHから右に線を引いた点が⑥のOになります。線分HOは切られたところです。 ここで、会話文のたろうさんの言葉がヒントになります。「ハサミで1回しか切ることができないという条件であれば、ハサミで切るまっすぐな線の上に切りたい部分が重なるようにもう一度折るしかなさそうですね。」 図6でハサミをいれた線分HOと重なる線分は⑥の図から、FCの中点Lから、GC上の点Nを結んだ線とわかります。 そして、HOとLNが線対称で対応する辺どうしとなるような対象の軸が、折り目となる直線です。JGで折れば、HOとLNは重なります。(ハサミを入れたところです) よって、答えは、点Jと点Gを結んだ 線JGになります。 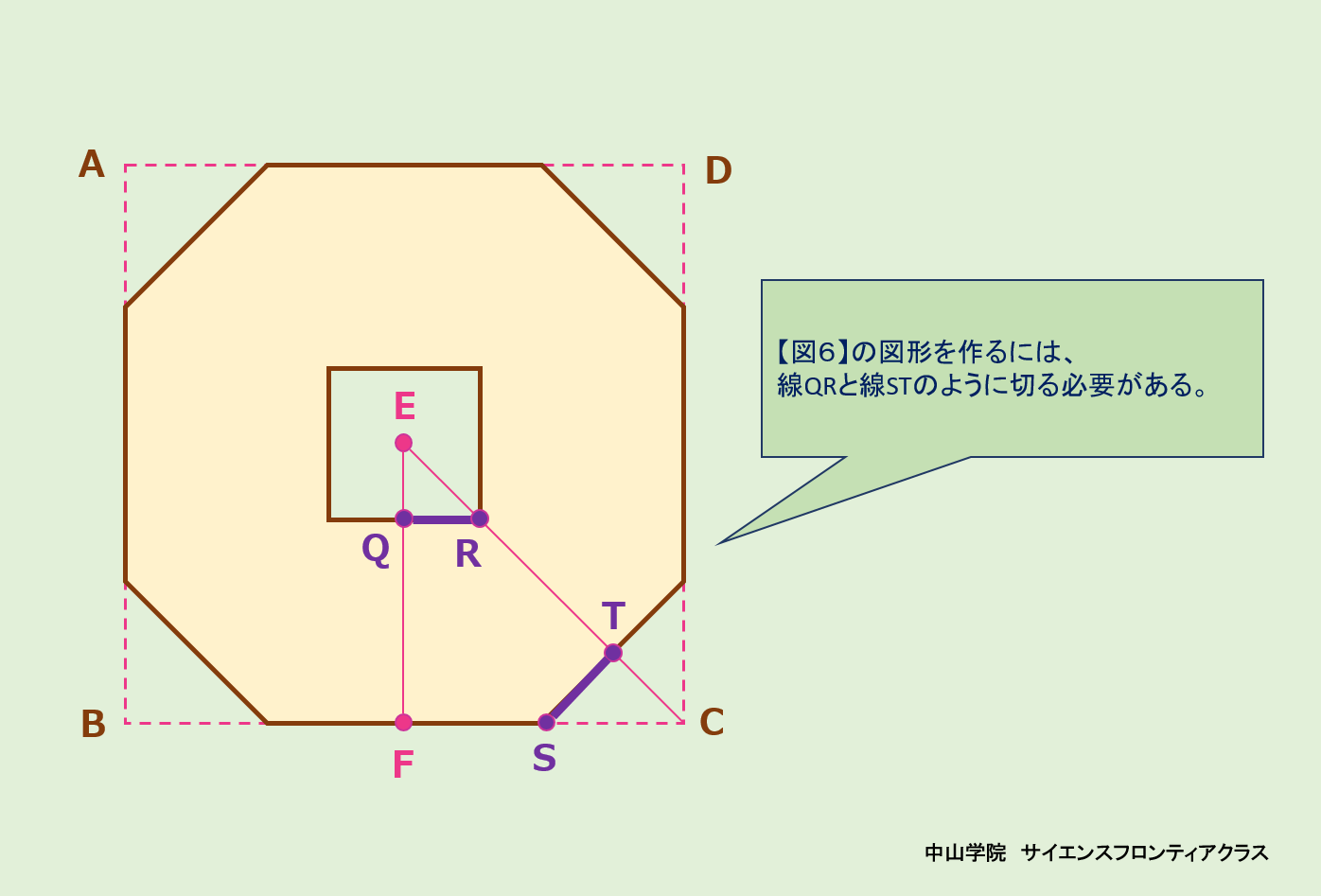 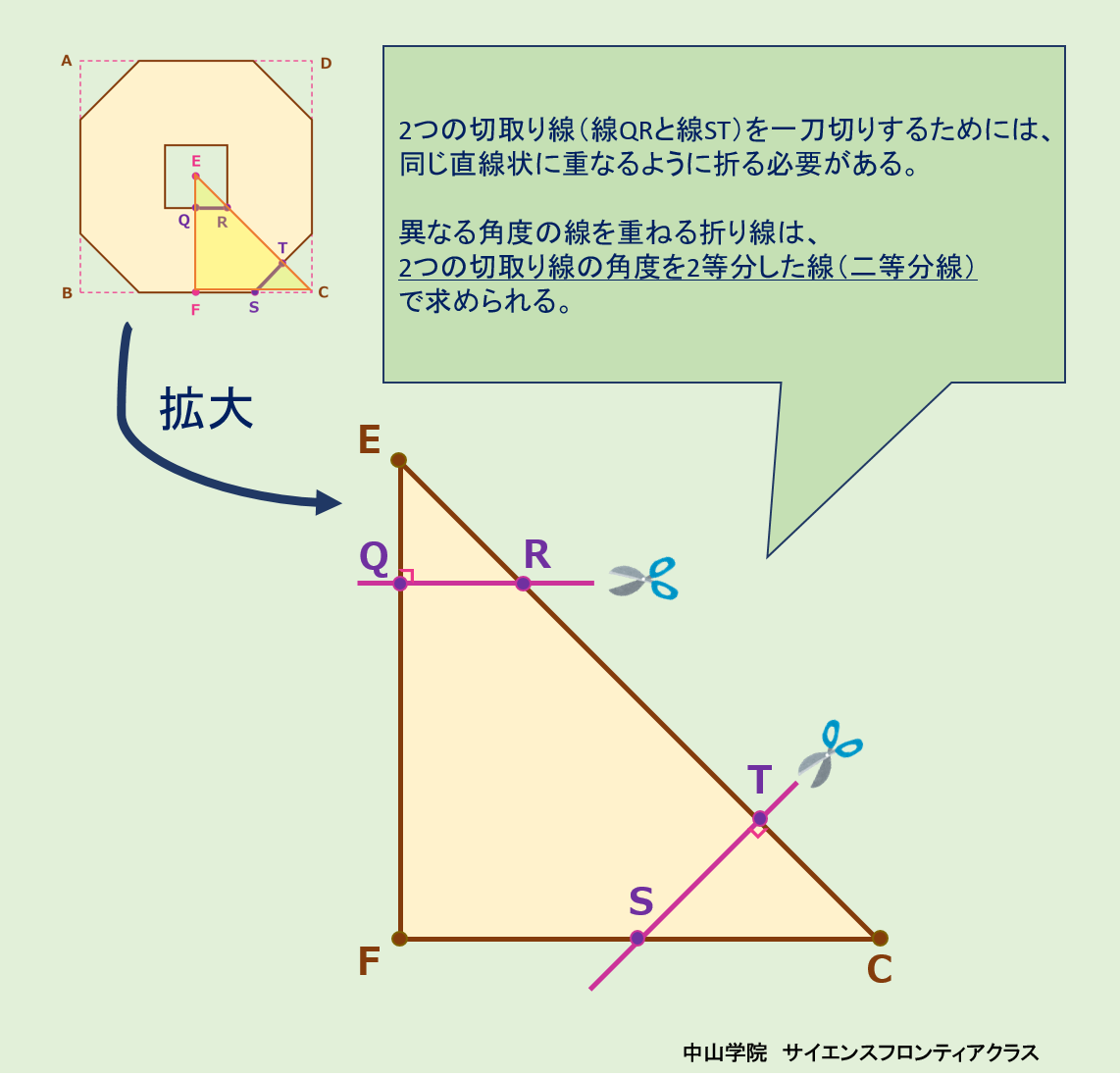 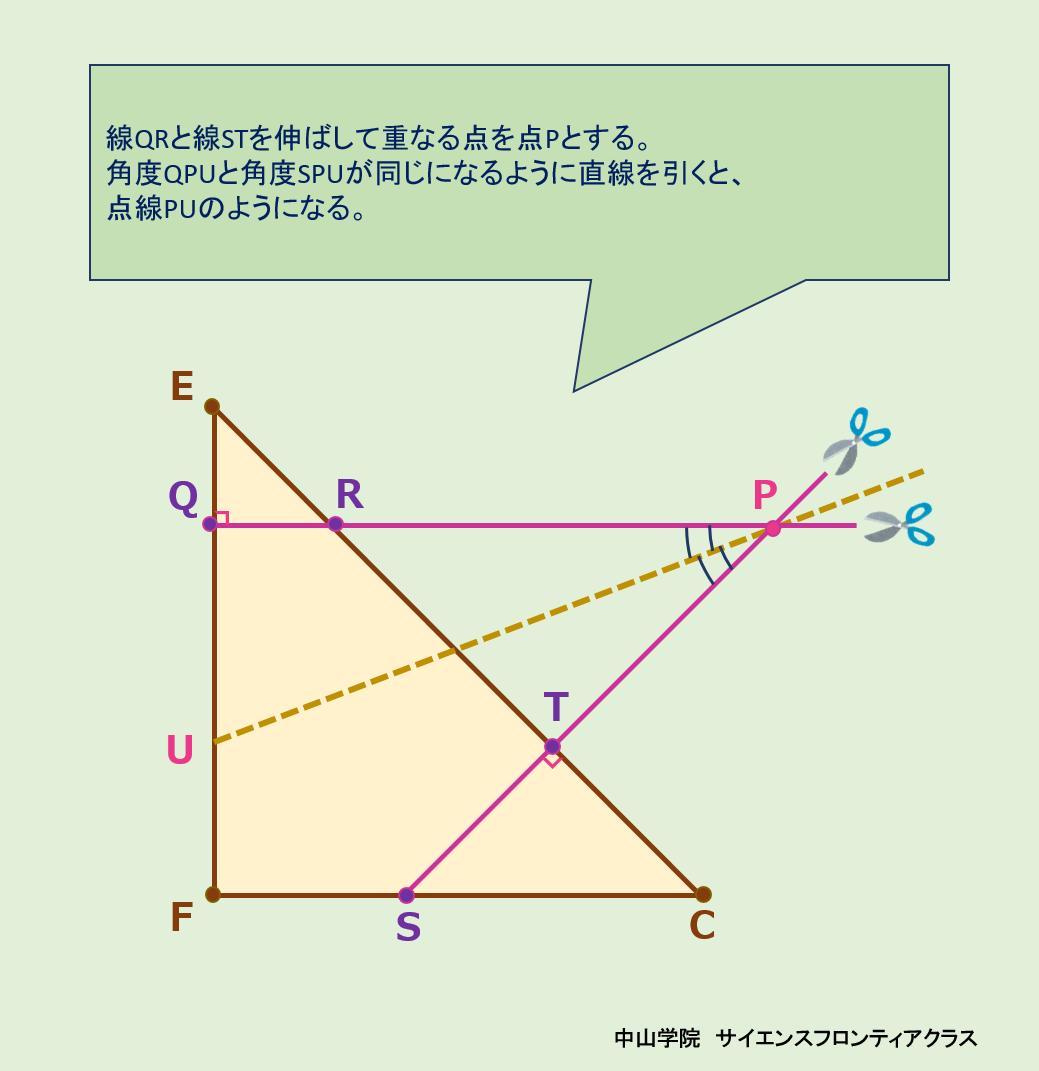 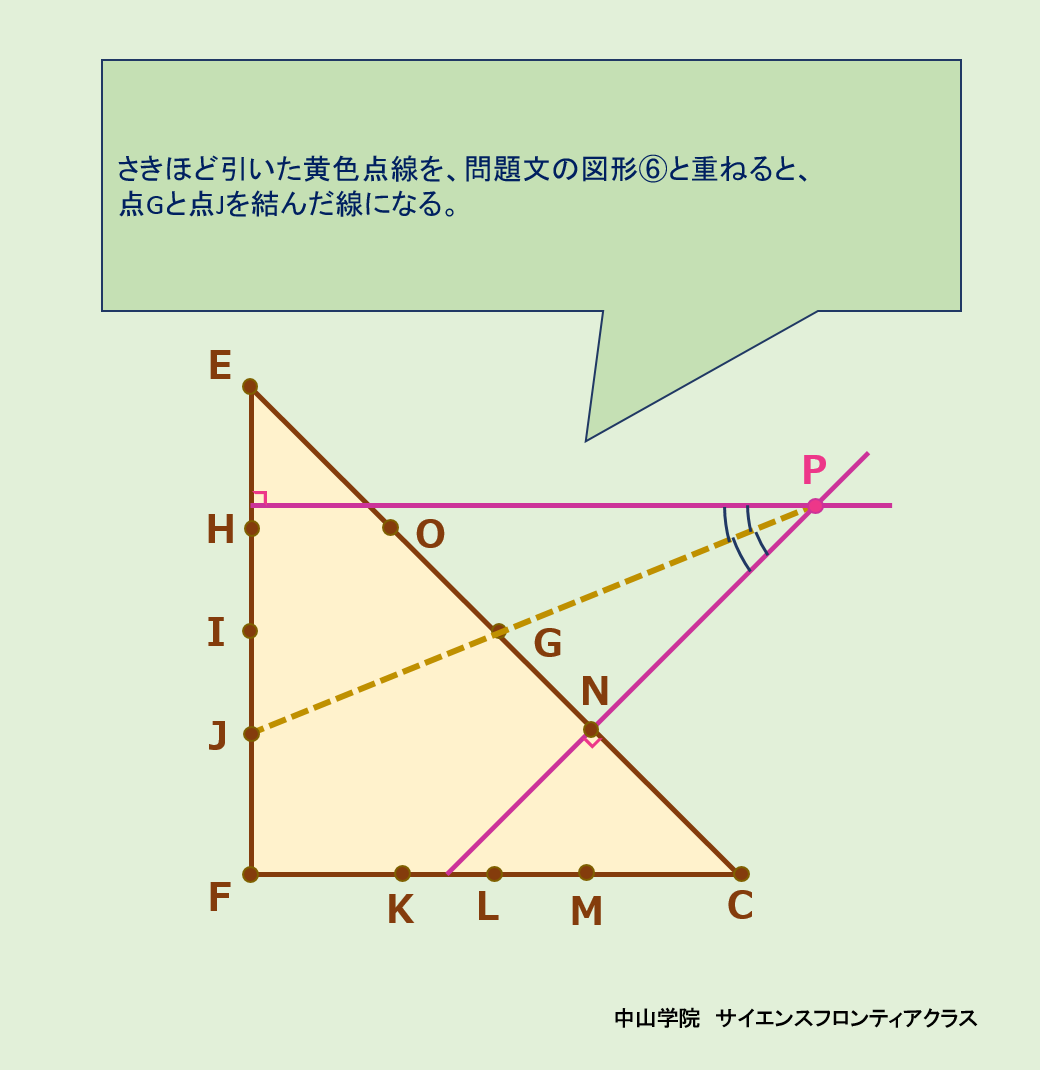 問題4 「会話文」中の( あ )( い )にあてはまる比を、それぞれ最も簡単な整数の比で表しなさい。 答えは、( あ )は 3 : 5 ( い )は 1 : 4です。 折り紙を開いていく順序を考えます。 図10・図12・図13から、QR=IF×2です。DP=QRなので、IFは、ICの半分です。 よって、( あ )は、EG:GB=HF:HC=1+4×0.5 : 1+4= 3 : 5 になります。 同様に、図から、DP=IC・・・① PQ=HI×2・・・②になります。また、DP:PQ=2:1なので 、①・②より、IC:HI×2=2:1・・・③となります。 ③の式で、内項の積=外項の積を使うと、HI×4=ICという式が導かれます。よって、(い)は、1 :4 です。 問題5 次の折り方(う)、(え)について、一刀切りをしたとき、どのアルファベットになるか、最も適切なものを、次の1~18からそれぞれ一つずつ選び、番号を書きなさい。 答えは、( あ )は 11 ( い )は 12です。 (あ) ⑦から逆に開いていきます。⑦から⑤までで、DCを下底とした台形ができます。それから③まででEFを軸としたアルファベットMの右半分になります。折り目がEFで、AとD、BとCが重なっているので、開くと①は11のアルファベットMになります。 (い) 同様に、逆算していきます。⑦の一刀切りでは、KCと平行な直線で切り、Bを含む折り紙を開くとあるので、H・K・Cを含む部分はなくなり、JはABと同じ側に移ります。そして、左側はABとそれに平行な辺を縦とした五角形になります。 ⑤では、その五角形の右上にADを下底とした等脚台形ができます。④と③でAD上に移ったEとFを元に戻すと、アルファベットPの穴の開いた下半分になります。②と①で、EFを対称の軸として、ADを広げると穴の開いた上半分が現れ、12のアルファベットPになります。 完 |